Relativity and satellite navigation

How to determine your position using radio signals and satellites – and what the theories of relativity have to do with it

An article by Markus Pössel

At sea or in the wilderness, precise positioning can be vital. But even in everyday life, there is not always a place or street sign nearby when the question comes up: Where are we now? The answer is readily available these days. A small device, not much bigger than a cell phone, is enough to determine your location within a few minutes – anywhere in the world, with an accuracy of a few to a few dozen meters:

The magic word is satellite navigation. The most well-known one is probably the U.S. “Global Positioning System”, abbreviated to GPS. GLONASS, the Global Navigation Satellite System, was set up as the Soviet counterpart to GPS and is now operated by the Russian Federation. Galileo, a European satellite navigation system, is now also available. The way these systems work is directly related to Einstein’s theories of relativity.

The circle of possible places

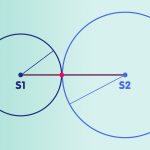
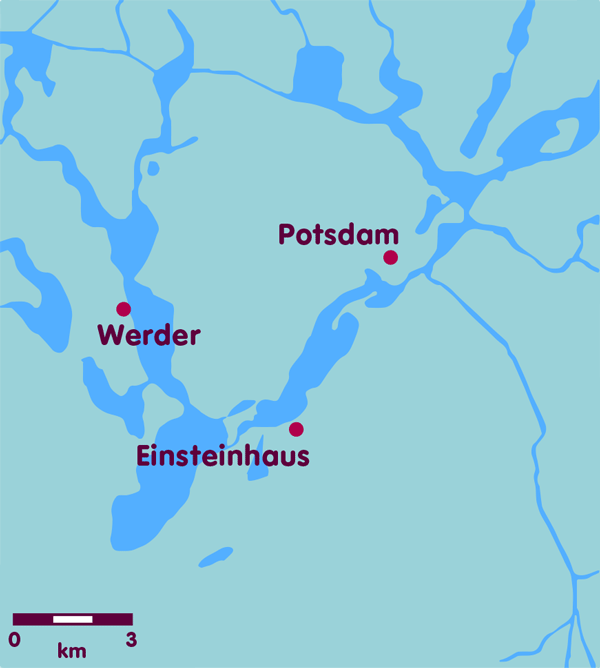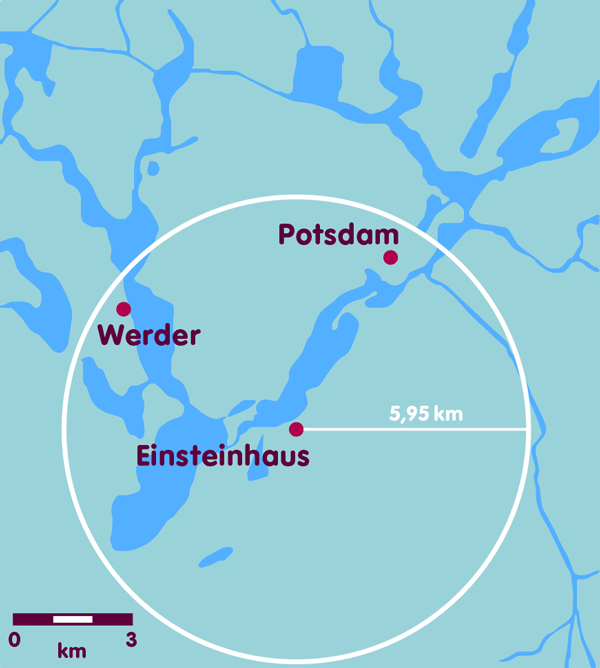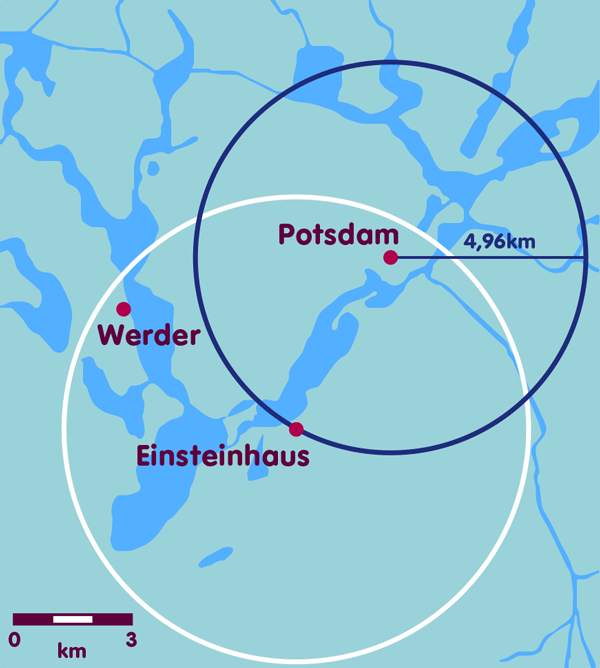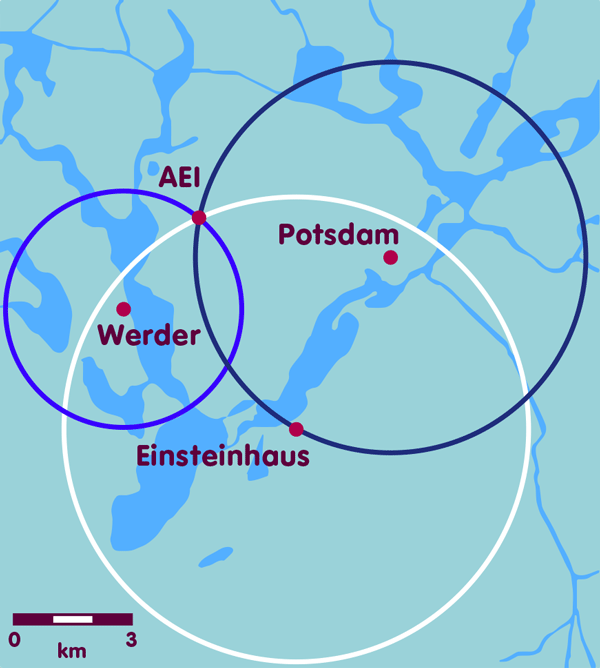
But one thing at a time. The first step toward satellite navigation is to realize that if you know your distance from a large enough number of known locations, you know your own location. This is easiest to see in the case of a two-dimensional plane – something we are used to from maps. For example, if I know that I am 5.95 kilometers away from Einstein’s summer house in Caputh, I can draw a circle on the map with a corresponding radius, whose center is Caputh (the red circle in the figure below). On this circle are all places which are 5.95 kilometers away from Caputh, thus also my location. If I additionally know that I am 3.04 kilometers away from the center of Werder, I can draw another circle on the map with a radius of 3.04 kilometers, whose center is Werder – the circle of all places that are 3.04 kilometers away from Werder, thus also my own location (the blue circle in the figure below). My own location is on both drawn circles, so on one of the two intersections. If I have at least a rough idea of where I am – for example, that I am east of Werder – and can thus exclude one of the two points, then I have thus clearly determined my location. If not, a third distance information provides clarity: It results in a third circle, for example the circle of all places which are 4.96 kilometers away from the city center of Potsdam (the green circle in the figure below). Unless there is a special case where the three centers of the circle all lie on one line, the intersection of the three circles clearly determines my location – in this example, by the way, the Albert Einstein Institute (AEI) in Golm, a district of Potsdam:

If we are not dealing with a two-dimensional plane, but want to determine a position in three-dimensional space, one additional information on distance is needed. The distance from a single known location A corresponds to the spherical area of all points in space which have the respective distance from A. The distance specification for a second place corresponds to a second spherical surface, so that our location must lie on the intersection circle of the two spherical surfaces. The spherical surface resulting from the distance indication for a third location generally intersects this intersection circle in its turn in two points; if necessary, the intersection with a fourth spherical surface – a fourth distance indication to a known location – shows which of the two points is our own location.

From time to distance

So far, so good: If you know your distances to enough known places, you can also determine your own location. But how do you determine these distances? If we assume that the rules of Einstein’s Special Theory of Relativity apply in our universe, there is a simple solution: According to this theory, the speed of light has the same constant value of 299,792,458 meters per second for every observer (more precisely: for every inertial observer). Now we set up a clock and a radio transmitter at each of the reference locations. We ourselves also carry a clock, plus a radio receiver, and we have made sure that all of the mentioned clocks are in sync. Each of the radio transmitters continuously emits a radio signal in all directions, which, like all electromagnetic radiation, propagates at the speed of light. The radio signal is, on the one hand, a time clock signal, controlled by the clock at the place of transmission. For example, radio stations might emit a time signal pulse every billionth of a second. On the other hand, the radio signal contains information, for example, in that particularly strong and somewhat weaker pulses follow one another like the dots and bars of a Morse code message. They encode from which reference location and at which time a certain pulse was transmitted. As a result, whenever our receiver receives a time signal pulse, we can read from which location and at what time this pulse was sent. The clock in our own receiver, on the other hand, tells us when the pulse arrived, and already, thanks to the constancy of the speed of light, we know the distance to the reference location. For if we know the time of transmission and reception, we also know how long the pulse took to travel to us. Travel time times speed of light results in the distance to the reference location.

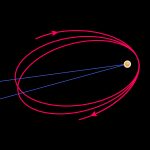
With this knowledge, we can already construct a simplified version of a satellite navigation system. Our reference locations are satellites orbiting the earth. The following figure shows six orbits for 24 satellites, or more precisely: the basic configuration of the Global Positioning System (GPS), which ensures that there are enough satellites in the sky at any time as seen from any location on the Earth’s surface. The orbits are drawn to scale relative to the Earth, but the satellites themselves are greatly magnified.

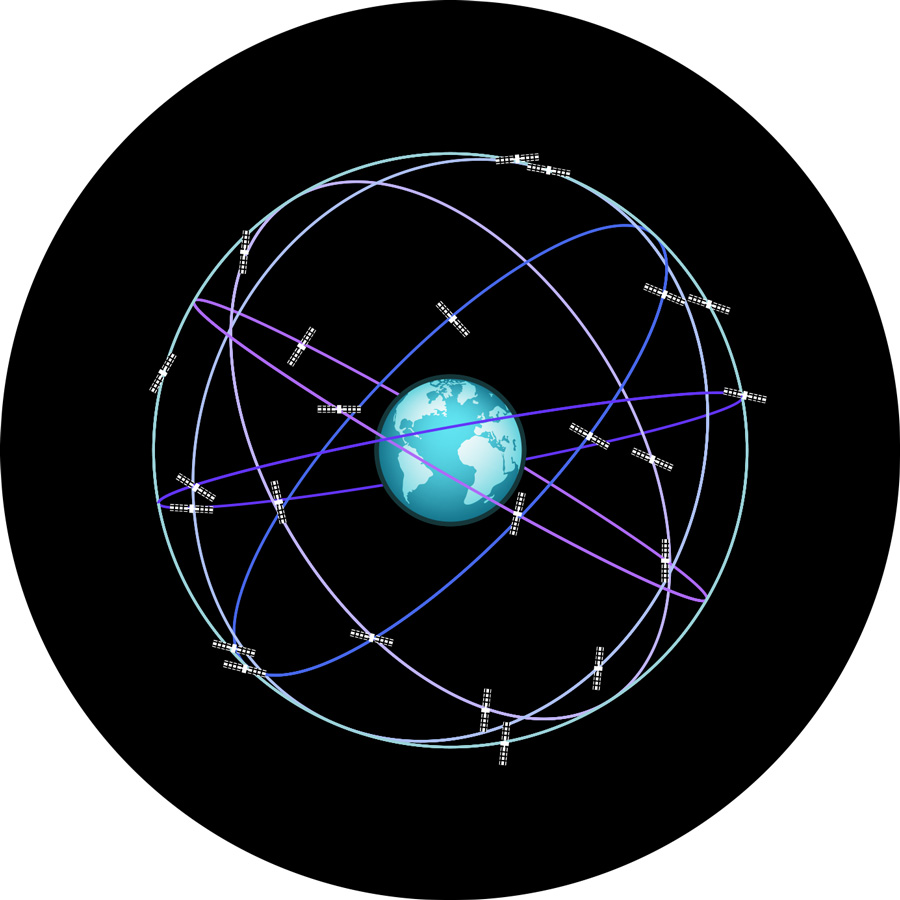
Approximately 20,200 kilometers above the Earth, the satellites move along their nearly circular orbits at an orbital speed of about 14,000 kilometers per hour. Each of the satellites transmits a time signal in which a number of additional pieces of information are encoded. The first is the time at which the signal is transmitted, determined by an atomic clock on board of the satellite, the rate of which is also constantly monitored by ground stations. Secondly, the orbit data for the satellite in question, also kept constantly up to date by ground station monitoring.

A receiving device on the ground can detect these signals and evaluate the information they contain. If an atomic clock were also built into the receiving device, perfectly synchronized with the satellite clocks, the position determination would actually proceed as in the step-by-step explanation above: The difference between the time of transmission and reception, multiplied by the speed of light, results in the distance to the various satellites. The locations of the satellites at the time of transmission are known: They can be calculated directly from the orbit data provided in the signal. Distance measurements to three satellites already limit the possible location of the receiver to two points in space. Thanks to the additional information that the location sought is not somewhere out in space, but close to the Earth’s surface, it is possible to decide which of the two possibilities is the correct one.

However, miniaturized atomic clocks that are affordable for large parts of the population are still a dream of the future. So inaccurate time readings are a considerable problem. Even a clock that was off by only a millionth of a second would result in an error of several hundred meters in determining satellite distances, with corresponding consequences for location determination. Favorably, however, there is a procedure to determine not only the location but also the time with the help of the satellite signals. For this, one more satellite is needed than for the determination of only the position. A more detailed explanation is given in the spotlight topic Time determination with radio signals – from radio-controlled clocks to satellite navigation. Briefly put, the additional condition that the range sphere around the fourth satellite should also intersect with the intersection of the other three range spheres allows the determination of the one missing parameter, namely the time at the receiving location.

Reference systems

However, even with this additional step we are not yet finished – even if one neglects, for simplicity, practical interfering factors like the influence of the Earth’s atmosphere on the satellite signals, with which the operators of navigation systems have to deal. For so far, our reasoning has assumed that the laws of special relativity apply, in particular the principle of the constancy of the speed of light. This was the only way to determine the distance to the satellite simply by multiplying the speed of light by the time difference. In reality the situation is more complicated: On the one hand there is the Earth and its gravitational influence on clocks and radio signal propagation, on the other hand there are the Sun and the other planets, and the satellites do not fly through space without forces, but are forced into a circular orbit by the Earth’s gravity. Favorably, most of the effects that cause deviations from special relativity do not matter at the present accuracy of satellite navigation (more information is given in this footnote). Instead, a closer look reveals: It is possible to introduce a fictitious reference system whose space zero point is at the center of the Earth, whose space distances are to a good approximation the same as in the real Earth environment, and in which light actually has the usual constant velocity. This fictitious system, in which we can calculate distances just as directly from time differences of light or radio signals as we have assumed in the explanation above, is also called earth-centered inertial system. Within the scope of the measurement accuracy necessary for satellite navigation, the light signals actually move through space at a constant velocity with respect to this system, and the navigation satellites move on the elliptical orbits well known from celestial mechanics.

Time dilation

This preparation brings us to the relativistic effects that actually play a role in satellite navigation. They result from the fact that in the theories of relativity, there isn’t a single time. How fast or slow time passes, and in particular how fast or slow clocks go, depends partially on how they move. For example, with respect to our Earth-centered inertial frame, the time dilation of special relativity applies: clocks moving relative to this frame go slower compared to clocks that rest in it. On the other hand, as shown for example by a comparison with the help of light signals, clocks in the vicinity of a massive body like the Earth go slower the closer they are to the body (gravitational time dilation).

Different classes of clocks are important in satellite navigation. First, there are the atomic clocks on Earth. With their help, physicists determine the unit of time in our Earth-centered inertial system – according to the definition of the international system of units SI: One second in our reference system is defined by the frequency of a certain atomic transition of cesium-133 under the conditions under which such a transition takes place in an atomic clock here on the Earth’s surface. Through the standard value of the speed of light (299.792.458 meters per second), also the unit of length meter of our reference frame can be determined. In these units, in this reference system, the astronomical calculations of the satellite orbits are performed.

Second, there are the atomic clocks on the satellites. With them the time measurements are accomplished, which lead to the position determination.

However: Who simply uses the same atomic clocks as on Earth as satellite clocks, without caring about relativistic effects, makes a mistake. Under conditions on Earth, the atomic clocks in question may just show the unit of time we have chosen for our Earth-centered inertial frame. But when we shoot them upward into the orbit of the navigation satellites, they run a tiny bit faster than on Earth. This results from two opposing effects: First, the flying clocks have a much higher orbital velocity compared to clocks on the Earth’s surface, so they are somewhat slowed down due to the time dilation already described in special relativity. On the other hand, the clocks are noticeably farther away from the Earth – due to the less strong gravitational time dilation, they thus go somewhat faster than clocks of the same design on Earth. The second effect predominates, and overall, a clock on one of the navigation satellites is faster than an identical clock on Earth.

From the time coordinate in our earth-centered inertial system, which was defined by the earthly clocks, the display of the satellite clocks therefore deviates gradually more and more. If you insert this wrong time into the formulas for the satellite orbits in order to determine their position, you will get a result that is all the more falsified the longer the navigation system has been in operation – the satellites are in reality at a slightly different orbital point than predicted with this wrong time. Also the distance measurements (and the definition of the meter) are directly linked to the unit of time – if you multiply the wrong atomic clock seconds by the speed of light to determine the distance of the satellites, you get a slightly different value than in the earth-centered reference system we have chosen.

The operators of the navigation system GPS have solved the problem in a technically quite simple way: The clock frequency of the atomic clocks is adjusted in such a way that they would run somewhat slower on Earth than the reference clocks on the basis of which the second is defined. When the atomic clock adjusted in this way flies through space on board one of the GPS satellites, the change in clock frequency just compensates for the relativistic rate acceleration. With this corrected running speed, the atomic clock reliably displays the time of our earth-centered inertial system. The result: reliable positioning, accurate to within a few meters, but which would not work if the effects of Einstein’s theories of relativity were disregarded.

Further Information