From light clocks to time dilation
A simple thought experiment with light clocks – clocks in which light keeps stroke – allows the derivation of time dilation.
An article by Markus Pössel
Suppose I am drifting freely through space with a space station, far away from all larger masses. In this case, physicists would consider me an inertial observer, and thus the two basic postulates of special relativity would apply to me. In particular, the postulate of the constancy of the speed of light: light travels at the constant speed of 299,792,458 meters per second, or about 300,000 kilometers per second – I will use this rounded value in the following because it simplifies the calculations considerably. Where these postulates hold, a basic effect of special relativity can be derived quite easily with a thought experiment: time dilation.
Time measurement with light running up and down
The constancy can be exploited to construct a special kind of clock in thought, a so-called light clock. Its operating principle is very simple: Two mirrors are placed at a constant distance from each other. A light pulse runs up and down between them. Each arrival of the pulse at the upper mirror corresponds to a “tick” of the clock. A detector receives the pulse when it reaches the upper mirror and passes this information on to a counter, which counts how many times the pulse has already arrived – in the following simple animation only from 0 to 9, but in a more realistic light clock continuously:
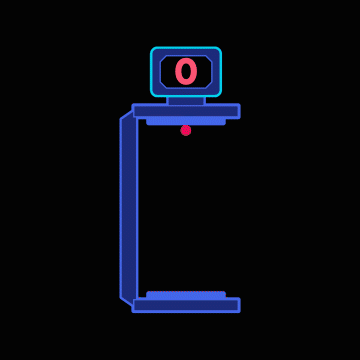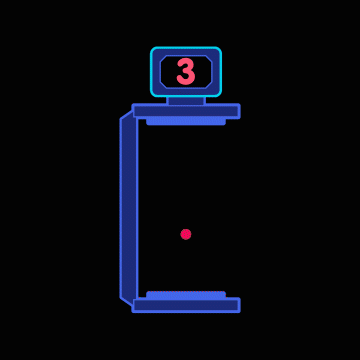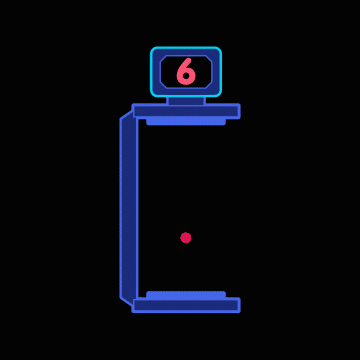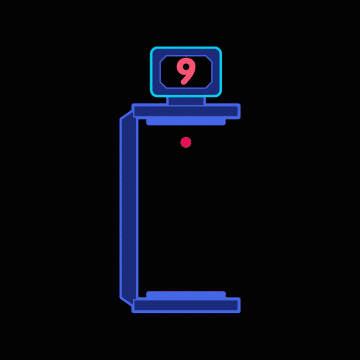
If the mirrors are placed at a distance of 150,000 kilometers, our light clock ticks exactly once per second. The second cycle displayed in this way is the same one that we would measure with any other good clock – after all, one second is just the time it takes light to travel a distance of 300,000 kilometers at its speed of 300,000 kilometers per second, i.e. two times 150,000 kilometers – the distance between the mirrors back and forth.
At shorter mirror distances, the clock ticks faster; at a mirror distance of only 15 centimeters, for example, our clock would tick every billionth of a second. For a real clock, such a short tick would be advantageous – it would then be possible to measure fractions of a second with great accuracy.
Light clock in motion
Now let’s consider a second space station, also floating freely in space and moving past my own station at a constant speed. An observer on this space station is also an inertial observer. Also for him the principle of the constancy of the speed of light is valid. He too can take advantage of this to construct a light clock by placing two mirrors at a constant distance from each other and equipping one of them with a counter. If he chooses a distance of 150,000 kilometers, then his light clock will also beat in beautiful unison with all his other clocks every second.
It gets interesting when I examine this light clock moving past me on board of the other space station. The simplest case is when the light clock is perpendicular to the direction of motion. It can be shown that even in the special theory of relativity, observers moving relative to each other agree about distances perpendicular to the direction of motion. If the inhabitant of the passing space station attaches the two mirrors of his light clock in the distance of 150,000 kilometers, then I will also obtain 150,000 kilometers upon measurement of the mirror distance of the passing light clock with my own measuring stick.
How long does it take from my perspective for the light of the moving light clock to run from the upper to the lower mirror and back? In other words: How much time passes from my point of view between two successive ticks of the moving light clock? The answer is given by the following animation, which shows two identical light clocks. Instead of the counter, these light clocks have an indicator lamp that flashes briefly each time the light pulse arrives at the upper mirror. At the top of the picture you can see my own light clock, which is resting relative to me. Below, the moving light clock flies by at about 86.7 percent of the speed of light:

Apparently, from my point of view, the moving light clock moves much slower than my own identical light clock: Between two ticks of the light clock (corresponding to the indicator light blinking twice), twice as much time elapses for the moving clock as for my own. In other words: In the period between the first flashing of the indicator lamp of the moving clock (on the left side of the picture) and the second flashing (on the right side of the picture), the resting clock has flashed three times altogether!
Different lengths
What is the reason for this discrepancy? Why does the moving light clock blink more slowly?
The constancy of the speed of light is valid: Light moves with the constant speed of 300,000 kilometers per second. If I divide the distance the light has traveled on its way from the upper to the lower to the upper mirror by this speed value, I get the time the light needed for a round trip.
We have already made this calculation for the light clock at rest. There, from our point of view, the light runs vertically downwards and then vertically upwards:
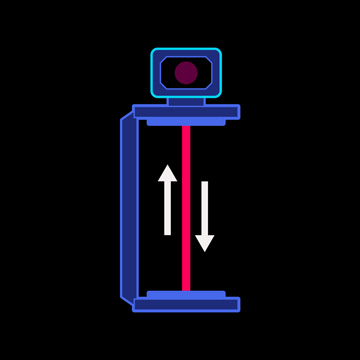
The time needed for this is therefore twice the mirror distance divided by the speed of light. With the assumed mirror distance of 150,000 kilometers and the value 300,000 km/s for the speed of light, the running time is exactly one second.
Differently with the moving light clock. Its mirrors move, judged from my space station, with constant speed to the right. Light, which travels from the upper mirror to the lower mirror and back to the upper mirror, therefore moves inevitably in zigzag – from the original place of the upper mirror to that place a little further to the right, to which the lower mirror has moved until the arrival of the light, and further to that place still further to the right, which the upper mirror has reached, when the light finally arrives again at the top. The light path is thus as shown in the following figure, which also includes three snapshots of the moving light clock:
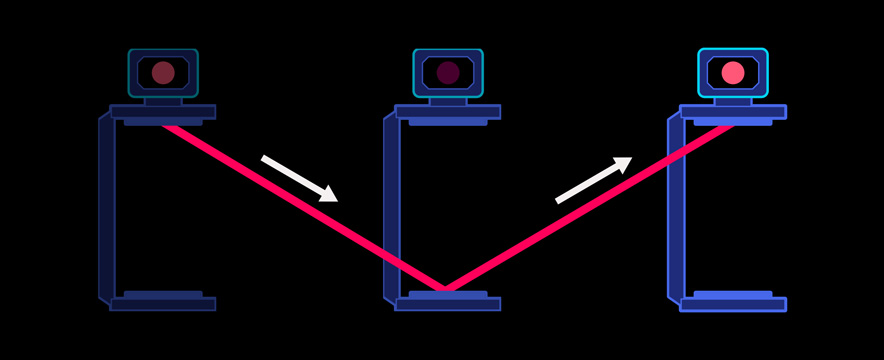
Such a zigzag path is much longer than two times the vertical mirror distance – after all, in addition to the distance in the vertical direction, there is also a horizontal distance that the light has to overcome. In our example, in which the moving clock rushes along at 86.7 percent of the speed of light, the zigzag path is exactly twice as long as the vertical up-and-down.
But if the distance which the light covers during its round trip in the moving light clock is, judged from my space station, greater than 300,000 kilometers – greater than twice the perpendicular distance – then also the time the light needs for the round trip must be longer than one second. One “second” measured on the moving light clock is thus longer than one second measured on my own light clock, which is at rest relative to me – in the example illustrated above, it takes twice as long. Accordingly, from my point of view, the moving light clock goes only half as fast as the light clock in my own space station.
As already said: All clocks resting relative to the moving space station have the same beat as the moving light clock. All clocks resting in my own space station have the same beat as my own light clock. The consideration of the light clock is therefore only an example for a much more general circumstance, the time dilation of the special relativity: Judged from my space station all clocks of the space station moved relative to me run slower than my own clocks. Just as the moving clocks run slower, all processes on the other space station also run slower for me – five-minute eggs take longer to cook and still have the right consistency in the end, and the pianist on board the other station who plays the Minute Waltz takes considerably more time to do so than is normal performance practice.
Further Information
Time dilation is the subject of a number of other spotlight topics in the category of special relativity. The most amazing property of time dilation is its reciprocity: In the above example, from the point of view of an observer, the clocks on my space station would run slower than his own. The spotlight topic The Dialectic of Relativity is devoted to this aspect in a rather fundamental way, while Time Dilation on the Road explores a geometric analogy that can be used to easily demonstrate reciprocity. The situation gets a bit more difficult when accelerations come into play – in that case, we get very quickly to what is sometimes called the twin paradox. More about this can be found in the spotlight topic The case of the travelling twins and, again as a geometrical analogy, in Twins on the Road.
Caution, fake light clock!
Occasionally one sees animations with light clocks ticking twice as fast as the ones shown here. For them the counter counts when the pulse reaches the upper mirror and also when it reaches the lower mirror. Such light clocks lead the simple functional principle ad absurdum, because how does the counter know when the pulse arrives at the lower mirror? This information would first have to be laboriously transferred from the lower mirror to the counter. But this transmission cannot be done faster than the speed of light. In particular, the information would not reach the counter before the light pulse itself already arrives again at the upper mirror.
Colophon
is the managing scientist at Haus der Astronomie, the Center for Astronomy Education and Outreach in Heidelberg, and senior outreach scientist at the Max Planck Institute for Astronomy. He initiated Einstein Online.
Citation
Cite this article as:
Markus Pössel, “From light clocks to time dilation” in: Einstein Online Band 13 (2021), 1004