Searching for the quantum beginning of the universe

About attempts to understand the beginning of our universe using different approaches to quantum gravity

An article by Jorma Louko

Suppose that we have at hand a quantum theory of all the forces of nature, including gravitation. What would we hope to do with this theory?

As one example, the theory should predict what happens in the innermost regions of a black hole formed by the collapse of a star – regions in which matter and energy are compressed to a density at which quantum gravity effects should become important. As a second example, the theory should predict what happens when elementary particles collide at energies so large that the quantum nature of spacetime plays a significant role in the collision dynamics. In some theories of quantum gravity this energy is within the reach of particle accelerators that are currently under construction, and the theories indeed predict how frequently miniature black hole pairs would be produced in the accelerators. In less optimistic theories the threshold energy is of the order of Planck energy, which is far beyond the capabilities of accelerators that could be built with current technology, but even in this case the theory should provide a prediction that a technologically vastly more advanced civilization could in principle test in their gigantic accelerators.

These examples have an important aspect in common. They start out with a situation that can be described without a theory of quantum gravity – an ordinary star, say, or two particles heading for a collision. Quantum gravity is needed only to describe how the situation then develops – how the collapsing star forms the interior of a black hole, or what happens in the high energy density region where the particles collide. To summarise: In these examples the initial conditions can be described in terms of classical spacetime, while a theory of quantum gravity is needed for predicting the subsequent evolution.

But what could a theory of quantum gravity predict about the earliest universe?

The need for an initial quantum state

The classical big bang cosmological models describe gravitation by Einstein’s general theory of relativity. These models are able to treat the matter content of the universe quantum mechanically where appropriate, but they do not take into account the interplay of quantum theory and gravity. While the models have been successful in describing most of the history of our universe, they become ill-defined at the very beginning of the universe – at the big bang singularity. At this singularity, both the curvature of space and the density of matter are infinite – a state of affairs that is unacceptable for a physical theory.

It is widely expected that the infinities of the big bang singularity will no longer be present in a theory in which also the dynamics of spacetime is treated quantum mechanically. Here, however, the situation is fundamentally different from the two examples mentioned above. The earliest universe was presumably quantum mechanical through and through, and we can no longer describe its initial conditions in a classical language. We must instead treat the whole early universe as a quantum system and formulate its initial conditions in the language of quantum mechanics. We need to ask the basic question of quantum cosmology: What was the initial quantum state of the universe?

Quantum gravity theorists have not shied away from the challenge. At present there are some half a dozen contenders for a principle that would single out, from all the quantum states allowed by the dynamical laws of quantum gravity, the initial quantum state of our universe.

A universe without a (past) boundary?

Perhaps most studied among the proposals for the initial state of our universe is the “no-boundary” proposal of James Hartle and Stephen Hawking, dating from 1983. To state this proposal, we first need to recall that in Feynman’s path-integral formulation of quantum mechanics, the probability of the universe to evolve from an initial state A to a later state B is calculated using a kind of sum over all conceivable ways this evolution could have taken place – over all possible histories leading from state A to state B. (For more information on path integrals, see the spotlight text The sum over all possibilities.) Now, Hartle and Hawking proposed a specific initial boundary condition for the histories that describe our universe. The gist of the proposal can be seen by considering a simplified model universe with only one space dimension, evolving over time from an initial state. We take space in this model universe to be shaped like a circle:

A simple space shaped like a circle

If we plot the evolution of space over time, the circle traces out a sort of tubular, two-dimensional surface. The following picture shows one such surface, in which the universe begins in some initial state (the circular boundary at the earliest time, traced in red) and, over time, expands (reading from bottom to top as time progresses, the circles stacked to form the two-dimensional surface get ever larger):

Evolving universe with past boundary

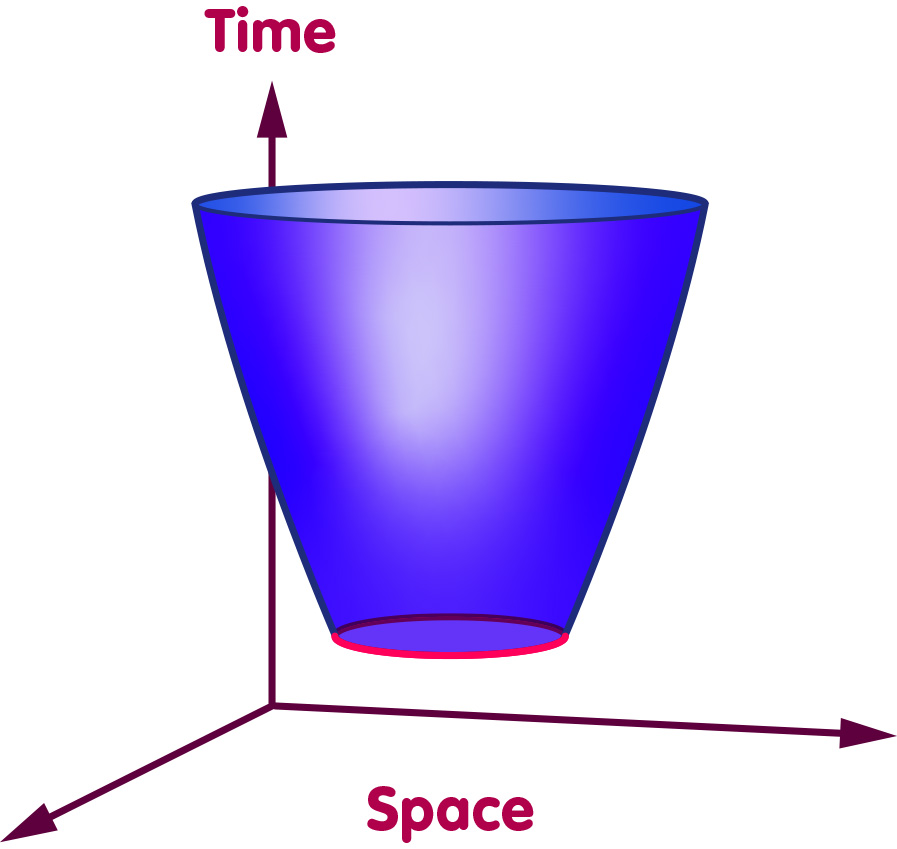
Another possibility would be a universe that starts at zero size, not smoothly, but with a kind of singular cusp, as pictured in the following image:

Evolving universe with past boundary

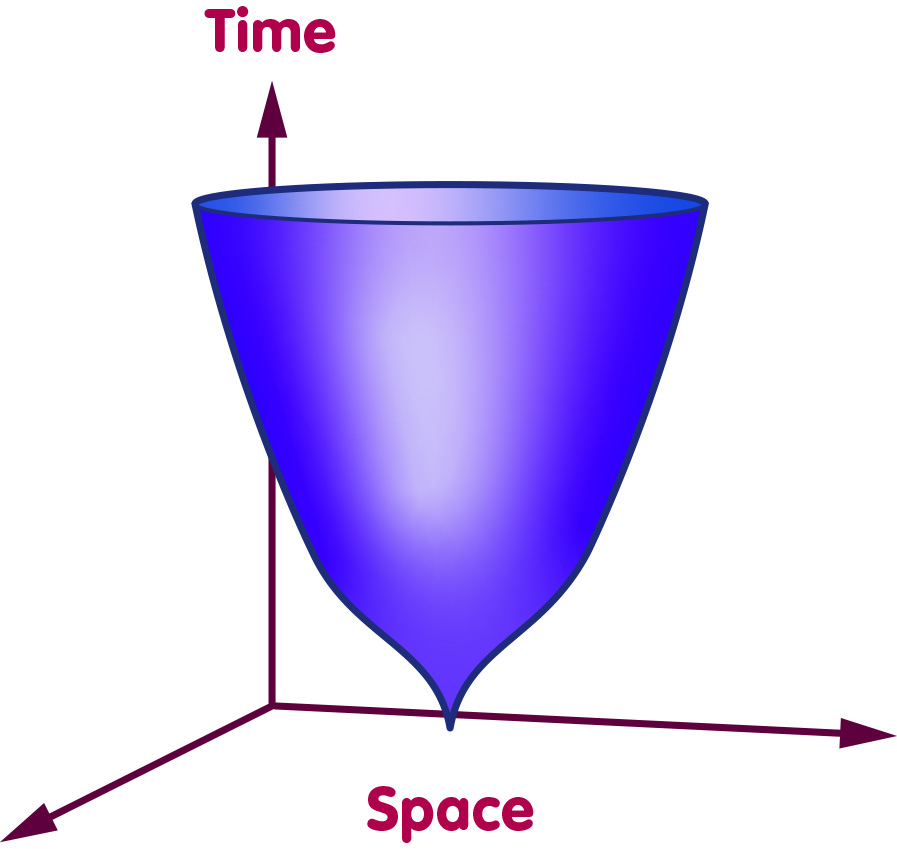
Hartle and Hawking’s proposal is that the initial state should have zero size but the evolution from this state should start smoothly, without any singularities. In our model universe this proposal would mean that the geometry at the initial state may not have a sharp end, such as the tip of a cone, but must instead be smooth, as in the following picture:

Evolving universe without past boundary and without singular beginning

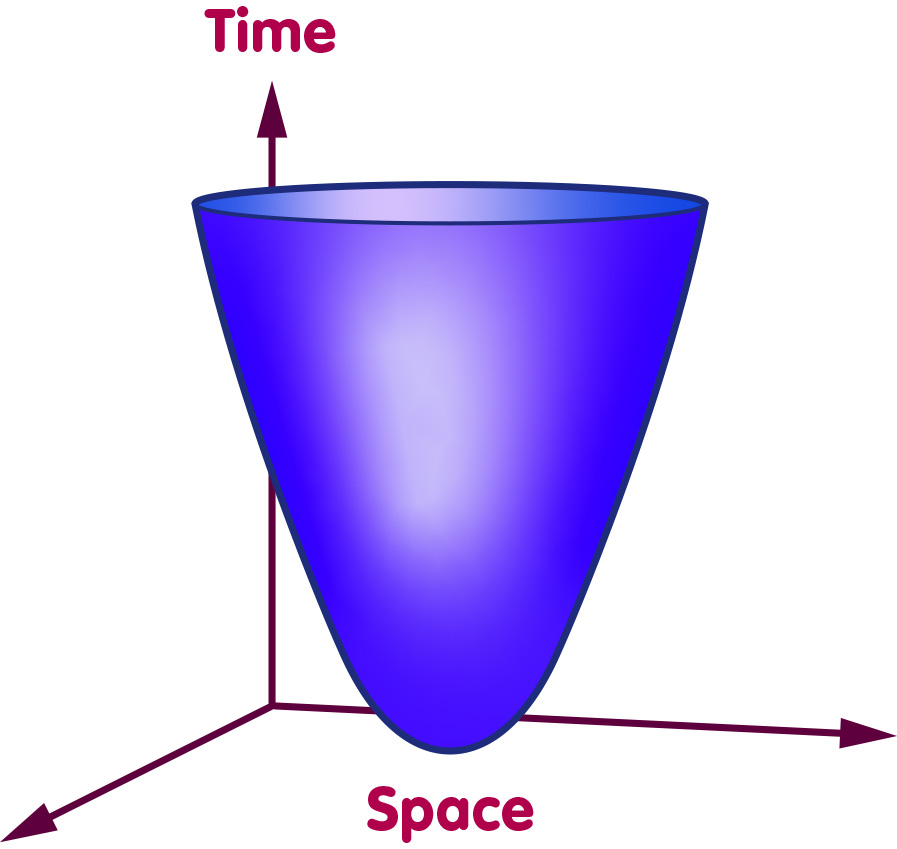
The boundary condition is thus that the spacetime histories have no initial boundary in the past. The only boundary that enters the path integral calculations is the boundary at the “present”, at the moment at which we make observations about the universe.

Tunnelling or symmetry?

Another proposal focusses on the observation that matter density at the classical big bang singularity is infinite. This means that it is classically impossible for the universe to start from zero size with finite matter density. In quantum mechanics, however, systems can undergo evolution that is classically forbidden, via a phenomenon called tunnelling. Classically, an object that does not have enough energy to climb over a hill will not get to its other side. But a quantum mechanical object that does not have enough energy to climb over a hill can nevertheless suddenly disappear from one side and appear on the other, as if instantaneously burrowing through a tunnel. One example of tunnelling is the spontaneous radioactive decay of certain atomic nuclei. Applying this picture to the beginning of the universe, one can thus envisage the universe as starting from zero size with finite matter density via a quantum tunnelling event. Implementations of this idea, known as the tunnelling proposal, have been advocated by Andrei Linde and Alexander Vilenkin.

Yet another proposal is based on the observation that the current rate of cosmological expansion appears to be the same in all spatial directions. While some cosmological models attribute this spatial large scale isotropy to dynamical evolution that has taken place since quantum gravity effects ceased to be important, a quantum gravity theorist would aspire to explain the isotropy directly by a quantum mechanical initial condition. This idea is implemented in the “symmetric initial condition” advocated by Heinz-Dieter Zeh, in which the zero volume singularity is postulated to have the maximum amount of isotropy compatible with Heisenberg’s uncertainty principle.

Open problems

The quantum state of the universe is ultimately an experimental question and should be resolved by comparison with observation. The ‘correct’ quantum state should at the very least be compatible with our present-day cosmological data, including the large-scale homogeneity and isotropy and the small observed anisotropies in the cosmic microwave background. Computing classical predictions of this sort from any proposed initial quantum state remains however a formidable challenge. There are two reasons for this. The first is technical, the second conceptual.

The technical reason is that making predictions from a given initial quantum state requires a sufficiently good control of the dynamical laws of quantum gravity. With our current candidates for a quantum theory of gravity, such a control exists if the theory is first classically specialised to a cosmological model universe that only incorporates a few parameters to describe the universe. For example, a homogeneous model universe sets the matter density to be the same at every point in space, describing thus the matter distribution by just one parameter, the average density. It takes however an infinite number of parameters to describe the real universe: The matter density in the real universe is not the same at every point in space. It is currently not well understood how accurately the quantum dynamics of quantised cosmological models, with only a few parameters, approximate the quantum dynamics of the real universe, with its infinite number of parameters.

The conceptual reason goes right to the heart of quantum theory. In the overwhelming majority of applications of quantum theory, physicists are dealing with a comparatively small quantum system on the one hand (a molecule, or colliding elementary particles), and on the other hand with measuring devices (such as particle detectors) that can be understood largely without resorting to quantum physics. The standard ways in which physicists extract predictions from quantum theory make use of this two-fold view of the world – here the quantum system, there the measuring device. In quantum cosmology, where the quantum system is the whole universe, this standard view is not valid any more. What is required is a working conceptual understanding of how to make classical predictions from a quantum state when even the observers are part of the quantum system that they observe. In the pursuit of this understanding, quantum cosmologists have in the past two decades found much common ground with laboratory quantum physicists whose experiments can in certain circumstances exhibit quantum mechanical behaviour between two ends of a room, or in some recent experiments even between the two banks of the Danube.

Further Information

For the basic concepts of relativity of interest for this spotlight topic, check out Elementary Einstein, in particular the chapters Relativity and the quantum and Cosmology.

Related Spotlights on relativity on Einstein-Online can be found in the sections Relativity and the quantum and Cosmology.

Colophon

Jorma Louko

is an Associate Professor of Mathematics at the University of Nottingham. His main research interest is quantum gravity, including quantum cosmology.

Citation

Cite this article as:
Jorma Louko, “Searching for the quantum beginning of the universe” in: Einstein Online Band 04 (2010), 02-1016

Definitioner

tunnelling (tunnel effect)

A quantum mechanical phenomenon that can be pictured as follows. Imagine a ball rolling towards a hill: Image of hill, ball rolling towards hill

Leaving quantum effects aside (in other words, in classical physics), we expect that what happens depends on the ball's energy: If the ball moves fast enough (i.e. has sufficient energy), it will climb the hill, pass the peak at B and roll down on the other side. If the ball is too slow, it will reach some maximum height and then begin to roll back down without having passed B. In the analogous situation for a quantum particle, there is another possibility. Even an incoming particle with enough energy to climb to the height A, but not to pass the peak B, can appear on the right-hand side of the hill at point C and continue onwards. Such a transition is called tunneling - it is as if the particle had taken a secret tunnel from A to C to avoid the forbidden peak around B and arrive directly at C. More generally, tunneling describes any transition from a state A to a state C that a quantum system can make, but that is forbidden to analogous systems in classical physics, since there, getting from A to C would only be possible by passing through a forbidden state B.

time

It is a fact of life that not all events in our universe happen concurrently - instead, there is a certain order. Defining a time coordinate or defining time, the way physicists do it, is to define a prescription to associate with each event a number so as to reflect that order - if event B happens after event A, then the number associated with B should be larger than that associated with A. The first step of this definition is to construct a clock: Choose a simple process that repeats regularly. (What is "regular"? Luckily, in our universe, all elementary processes such as a swinging pendulum, the oscillations of atoms or of electronic circuits lead to the same concept of regularity.) As a second step, install a counter: A mechanism that, with every repetition of the chosen process, raises the count by one. With this definition, one can at least assign a time (the numerical value of the counter) to events happening at location of the clock. For events at different locations, an additional definition is necessary: One needs to define simultaneity. After all, the statement that some far-away event A happens at 12 o'clock is the same as saying that event A and "our clock counter shows 12:00:00" are simultaneous. The how and why of defining simultaneity - a centre-piece of Einstein's special theory of relativity - are described in the spotlight topic Defining "now". With all these preparations, physicists can, in principle, assign a time coordinate value ("a time") to any possible events, and describes how fast or how slow processes happen, compared to that time coordinate.

surface

Geometric space with two dimensions. Examples include the plane or the surface of a sphere.

star

A cosmic gas ball that is massive enough for pressure and temperatur in its core to reach values where self-sustained nuclear fusion reactions set in. The energy set free in these reactions makes stars into very bright sources of light and other forms of electromagnetic radiation. Once the nuclear fuel is exhausted, the star becomes a white dwarf, a neutron star or a black hole.

space

In a strict sense: Space as we know it from everyday life: the totality of all locations in which objects can sit, with three dimensions. In a more general sense used by mathematicians, all kinds of sets of points are spaces - a line for instance, which has but a single dimension, or a two-dimensional surface, but also higher-dimensional spaces. Also, in such more general spaces, geometry can be different from the standard Euclidean geometry taught in high schools - such spaces can be curved.

spacetime

Already in special relativity, observers in motion relative to each other will not, in general, agree as to whether two events happen simultaneously, or as to how great is the distance between two objects. They do, however, agree as to what events there are, although not to when and where they happen. This observer-independent totality of all events is called spacetime. How spacetime is split into space and time can differ from observer to observer. Every-day space has three dimensions. Adding time adds another dimension - spacetime has four dimensions, all in all. We are used to the idea of a point in space - an object that has only one location and is completely defined once its space coordinates are given. In spacetime, a spacetime point is an object defined completely once its space coordinates and its time coordinate are given - which makes a spacetime point nothing but an elementary event. The idea of spacetime is, in addition to its role in special relativity, a building block of general relativity. Analogous to how a plane is flat, but the surface of a sphere is curved, in general relativity, curved or distorted versions of the simple, flat spacetime of special relativity play a role. Spacetime curvature, in general relativity, is intimately connected with gravity. For an introduction to the basics of both theories of relativity, check out the chapters Special relativity and General relativity in Elementary Einstein. Sometimes, it can be helpful to view spacetime in analogy to ordinary space - such analogies are explored in the spotlight topics Time dilation on the road (for time dilation) and Twins on the road (for the twin effect).

singularity

Irregular boundary of spacetime in general relativity - region where spacetime simply comes to an end. Often, such boundaries are associated with spacetime curvature growing beyond all bounds and becoming infinitely large - so-called curvature singularities (notably Ricci singularities or Weyl singularities - but there are exceptions (for instance a conic singularities). According to general relativity, a singularity exists inside every black hole, and the starting point of any universe described by a big bang model is a singularity as well. The occurrence of singularities is a failure of general relativity - and a strong indication that the theory is incomplete. Instead, one could describe the earliest universe and the interior of black holes using a theory of quantum gravity. More information about singularities can be found in the spotlight texts Spacetime singularities and Of singularities and breadmaking.

second

In the International System of units: the basic unit of time. Defined as a certain multiple of the oscillation period of electromagnetic radiation set free in a certain transition within the electron shell of atoms of the type Cesium-133.

quantum theory

The framework for formulating the physical laws that govern the world at microscopic length-scales - the physics of the micro-world, for instance of atoms, atomic nuclei or elementary particles, but also the physics of ultra-precise measurements such as those made by gravitational wave detectors.

The laws of quantum theory are fundamentally different from our everyday experience and from those of classical physics.

The first unusual feature is that, in many cases, quantum theory merely allows statements about probabilities. For instance, in classical physics, one can assign to every particle, at every point in time, a location and a velocity. Whosoever can measure those quantities precisely can, in principle, predict where the particle in question can be found at every point in the future. In quantum theory, all one can assign to a system of particles is an abstract quantum state from which can be derived no precise predictions, but merely the probabilities for detecting a specific particle at a given time in a given place. Whether or not one will really find the particle at that location is governed by chance.

The second unusual feature is a fundamental restriction placed on the exactness of certain measurements (Heisenberg uncertainty relation). For instance, the more precise one measures a particle's location, the less definite any statements one can make about its velocity.

The third feature is how quantum theory came by its name: A number of physical quantities in nature come in little packets, in quanta. For instance, according to quantum theory, electromagnetic radiation is made of tiny quanta of energy called photons.

Examples for quantum theories are quantum mechanics and relativistic quantum field theories such as Quantum electrodynamics or other parts of the standard model of particle physics.

quantum physics

Quantum physics comprises all theories, models, experiments and applications that are based on the laws of quantum theory.

quantum mechanics

In a more general sense: synonymous with quantum theory. In a more restricted sense: The quantum theory of particles moving under the influence of forces - wherein the particles are described as quantum objects, while the forces are not. An important application of quantum mechanics is the physics of the electron shells of atoms ("atomic physics", for short). Attempts to extend the quantum laws to govern the forces themselves lead to relativistic quantum field theories.

quantum gravity

Theory based both on the effects, concepts and laws of quantum theory and on those of general relativity. To date, no complete such theory exists; the best-known candidate theories are string theory and loop quantum gravity. Some information on the question of quantum gravity can be found in the chapter Relativity and the quantum of Elementary Einstein, starting with the page Border regions of gravity. Selected aspects of quantum gravity are described in the category Relativity and the quantum of our Spotlights on relativity.

quantum cosmology

According to the big bang models, the energy density of the very early universe was extremely high, with the contents of the observable universe compressed into a volume much smaller than that of an atomic nucleus. Under such circumstances, the effects of quantum physics and of general relativity should become equally important, in other words: This era of our cosmic evolution should be described using a theory of quantum gravity. Quantum cosmology encompasses all attempts to apply various candidate theories of quantum gravity to the physics of the early universe, and to describe the universe as a whole as a quantum system. More information can be found in the spotlight topic Searching for the quantum beginning of the universe. Some quantum cosmological applications of loop quantum gravity can be found in the spotlight texts Avoiding the big bang and Taming infinities with loops.

point

Elementary "building block" of geometrical entities such as surfaces or more general spaces. For instance, a surface is the set of all its points, of all possible locations on the surface, and all geometrical objects in that surface are defined by the points that belong to them - for instance, a line on the surface is the set of (infinitely many) points.

Planck energy

Natural unit of energy that can be obtained by combining the fundamental natural constants that govern spacetime, the strength of gravity and the quantum world: the gravitational constant, Planck's constant and the speed of light. Whenever elementary particles reach this kind of energy, in addition to the effects of quantum theory, the effects of general relativity should become important, in short: such situations could only be described adequately using a theory of quantum gravity. Compare: Planck length, Planck time, Planck mass.

nuclei (nucleus)

Extremely dense central region of an atom, consisting of protons and neutrons held together by nuclear forces. The number of protons determines what chemical element a nucleus represents. Typical diameter for atomic nuclei are in the region of a quadrillionth of a metre= 10^-15 metres. This makes nuclei about a hundredth of a thousandth as large as atoms.

molecule

Composite object consisting of two or more atoms, bound together by electromagnetic forces.

mechanics

Branch of physics dealing with the motions of objects and how they react to forces acting on them. Depending on the framework used, there is classical mechanics, relativistic mechanics and quantum mechanics.

matter

In general relativity: All contents of spacetime that contribute to its curvature: particles, dust, gases, fluids, electromagnetic and other fields. In particle physics: All elementary particles with half-integer spin, such as electrons and quarks, as well as their composites such as protons and neutrons, in contrast with force particles.

gravity

See gravitation

gravitation

In classical physics: An action-at-a-distance force by which all bodies that possess mass attract each other (see Newtonian theory of gravity), synonym: gravitational force. In Einstein's general theory of relativity: The fact that matter that possesses mass, energy, pressure or similar properties distorts spacetime, and that this distortion in turn influences whatever matter might be present. An introduction to the basic ideas of general relativity is provided by the section General relativity of Elementary Einstein. More information about the nature of gravity in general relativity can be found in the spotlight text Gravity: From weightlessness to curvature.

gravity (gravitation)

geometry

That part of mathematics concerning itself with surfaces or more general spaces as well as objects defined on such spaces, such as points or lines as well as the objects constructable from points and lines, such as triangles.

event

In the context of special or general relativity: Anything that is defined by a single point in time and a single point in space, i.e. something that happens at a definite time at a definite location. Synonym: spacetime point.

energy

Physical quantity with the special property that, in physical processes, energy is neither destroyed nor created, simply transformed from one form of energy to another. Some of the different forms of energy that are defined separately are kinetic energy, thermal energy and the energy carried by electromagnetic radiation. Processes that transform one form of energy into another take place in all machines we use in everyday life, from the engine of a subway train (electrical energy into kinetic energy of the train) to an electric blanket (electrical energy into thermal energy). One important consequence of special relativity is that energy and mass are completely equivalent - two different ways to define what is, on closer inspection, one and the same physical quantity. See the keyword equivalence between mass and energy.

elementary particles (elementary particle)

Within the commonly accepted models of physics, certain particles are not built of even more fundamental sub-particles - they are themselves elementary. Examples for elementary particles are electrons, quarks and neutrinos, while particles such as protons or neutrons consist of sub-units and are thus not elementary. The study of elementary particles is called particle physics, under which keyword some more information about the theoretical framework of elementary particles can be found.

dimension

The number of independent directions within a set of points, alternatively: the number of coordinates needed to give each point a unique name. This is rather abstract - time for some examples: A line is one-dimensional. There's only one direction to go on the line (the opposite direction isn't counted extra): Back-forth. A single number is sufficient to define a point of the line. For instance, on a motorway, given the statement "the accident happened 4 kilometres from the beginning of the I95 (or M1, or whatever)" is sufficient information for the rescue workers to know exactly where to go. Surfaces are two-dimensional, as there are two independent directions: back-forth and left-right, say. On the earth's surface, the two coordinate numbers geographical longitude and latitude uniquely define each location. The space that surrounds us is three-dimensional. There are three independent directions, say back-forth, left-right and up-down. In order to define a location in space, one needs to specify three numbers - for instance, two to specify where a house is located on the earth's surface (latitude/longitude, see above) and one floor number (or, more precisely, the height above the earth's surface). Adding time to the three space coordinates (a must for defining an appointment - where and when?), the result is four-dimensional spacetime. In order to define an event in spacetime, one needs to give four numbers: three of them determine where in space the event happens, the fourth gives the time where it happens. According to some of the models that have been studied as candidates for a theory of quantum gravity, our world should have even more space dimensions than the usual three. Some information about these extra dimensions can be found in the spotlight topics "Extra dimensions, and how to hide them", "Hunting for extra dimensions" and Extra dimensions and simplicity.

density

In a stricter sense synonymous with "mass density": The average density of matter in a region of space is the total mass of all matter contained in that region, divided by the region's volume. More generally, density can refer to other physical quantities as well. The energy density, for instance, is the total sum of energy localized in a region divided by that region's volume.

curvature

For a two-dimensional surface: criterion that allows us to decide whether that surface is a plane, or part of a plane (i.e. a surface on which the usual rules of high school geometry apply), or not. Two possibilities to define the curvature of a plane are the following: Sum of the angles of a triangle. In a plane, the sum of the three angles in a triangle formed by three straight lines is always 180 degrees. In a more general surface, the sum of the angles of a more general triangle formed by three straightest-possible lines (i.e. geodesics) can be larger or smaller than 180 degrees. The difference (the surplus or deficit), divided by the area of the triangle, is a measure for the curvature of that region of the surface. Second possibility: the circumference of a circle. In the plane, that circumference is equal to 2 times pi times the circle's radius. On a more general surface, it can be larger or smaller. The difference, divided by the third power of the radius, leads to the same measure for the curvature as the first definition. Simple examples for curved surfaces are the surface of a sphere (positive curvature, that is to say: sum of the angles in a triangle larger than 180 degrees, circumference of a circle smaller than 2 times pi times radius) and that of a saddle (negative curvature, that is to say: sum of the angles in a triangle smaller than 180 degrees, circumference of a circle larger than 2 times pi times radius). Curvature cannot only be defined for surfaces, but also for higher-dimensional, more general spaces or spacetimes. However, the generalized definition is substantially more complicated, and curvature is defined not by a single number, but by a set of numbers (that, together, form the "curvature tensor"). It's basic meaning, however, is the same: it measures the space's deviation from a flat space of the same dimension. For physics, an important aspect of curvature is its connection with gravity, as described in Einstein's general theory of relativity. Basic information about this can be found in the spotlight text Gravity: From weightlessness to curvature.

current

Matter in coordinated, flowing motion - think of water flowing in a pipe. An important example is the electric current associated with moving electric charges. Electric currents are the sources of magnetic fields.

cosmology

That branch of physics and astronomy dealing with the structure and development of the universe as a whole. At the core of modern cosmology are the big bang models based on Einstein's general theory of relativity. Their basic features are reviewed in the chapter Cosmology of Elementary Einstein. In order to describe the very early universe, it will be necessary to take the effects of quantum gravity into account - this gives rise to models of quantum cosmology.

classical

In physics, the word is used with two meanings. First of all, it denotes physical models or theories that take into account neither the effects of Einstein's theories of relativity nor those of quantum physics, for example classical mechanics. However, it is also used to denote models or theories that are not formulated in the framework of quantum physics; in that sense, general relativity is an example for a classical theory.

black hole

Region in space where a sufficient amount of mass is concentrated so that it forms a gravitational prison - a region into which matter or light can enter from the outside, but from which nothing that has once entered can ever leave. Basic information on this key phenomenon of Einstein's general theory of relativity can be found in the chapter Black holes & Co. of Elementary Einstein. Selected aspects of the physics of black holes and neutron stars are described in the category Black holes & Co. of our Spotlights on relativity. In Einstein's theory, black holes are truly black, due to the fact that no radiation or light can ever escape them. Once quantum theory is taken into account, this assumption no longer holds - on the contrary, it seems as if black holes should emit so-called Hawking radiation. However, for astrophysical black holes (that typically have more or even much more than one solar mass), that radiation would be undetectable, even if we could transport today's most sensitive sensors into the immediate vicinity of the black hole.

big bang

The big bang models are the foundation of modern cosmology. Firmly grounded in Einstein's theory of general relativity, they describe a universe that began in a very hot initial state and has expanded (and cooled down) ever since. They make precise predictions about nucleosynthesis in the early universe, the existence and properties of the cosmic background radiation, and the distribution of distant galaxies in the cosmos, which have been confirmed by astronomical observation. The word "big bang" has two different meanings. In a strict sense, the big bang is a spacetime singularity, a state of infinite density - the initial state the big bang models predict for our universe. In a more general sense, the term is applied to the earliest cosmic eras, in which the universe was exceedingly hot and dense. Further information about these two meanings and why it is important to distinguish between them can be found in the spotlight text A tale of two big bangs. The basic features of the big bang models are reviewed in the chapter Cosmology of Elementary Einstein. Selected aspects of cosmology are described in the category Cosmology of our Spotlights on relativity.